
منظور از بلندی صدا در واقع درک انسان از میزان بزرگی صدای شنیده شده است و واحد آن فون است. تلاش های اولیه که برای تعیین کمیت بلندی صدا در زمینه موسیقی انجام شد به این ترتیب بوده که سطوح «بسیار بلند»، «بلند»، «متوسط بلند»، «نرم» و «بسیار نرم» برای صدا تعیین شدند.
اما این اصطلاحات برای استفاده علمی به اندازه کافی دقیق نبودند و به شنوایی و عرف شخصی که از آنها استفاده می کند بستگی دارد. از طرف دیگر استفاده از شدت اندازه گیری شده یک صوت هم برای تعیین بلندی آن ساده به نظر می رسد، اما متاسفانه چنین رابطه ساده ای وجود ندارد.
بلندی صدا به تعداد تکانههای عصبی که در یک زمان معین به مغز میرسند بستگی دارد، اما از آنجایی که این تکانهها از نواحی مختلف حلزون گوش میآیند، با محتوای فرکانس سیگنال نیز تغییر میکنند.
حتی زمانی که یک سیگنال صوتی با شدت های مختلف شنیده می شود، بسته به وضعیت روانی و فیزیولوژیکی شنونده، تغییراتی از یک شنونده به شنونده دیگر وجود دارد.
واکنش مورد انتظار یک شنونده از بلندی صدا در یک محیط با آزمایش تعدادی از افراد، تحت یک سری شرایط کنترل شده تعیین می شود. میانگین یک گروه از شنوندگان به عنوان نتیجه مورد انتظار از یک شنونده در نظر گرفته می شود، فرضیه ای که در آمار به عنوان فرضیه ارگودیک شناخته می شود.
اندازه گیری های مقایسه ای در دهه های 1920 و 1930 توسط دانشمندان آزمایشگاه بل انجام شد. این آزمایشها بر روی گروهی از افراد با شنوایی خوب با ارائه مجموعهای از صداهای کنترلشده در فرکانس های مختلف انجام شده اند. با این حال، در مطالعه کلاسیک فلچر و مونسون که در سال 1933 منتشر شد، از تون های خالص (امواج سینوسی) با مدت زمان کوتاه استفاده شد.
این روش به این صورت بود که بلندی صدایی را که در یک فرکانس و دامنه خاص به شنونده ارائه میشد، با یک آهنگ مرجع ثابت در 1000 هرتز با دامنهای که در فواصل 10 دسیبل بین 0 تا 120 دسیبل تنظیم میشده، مقایسه شده اند. آهنگ ها با استفاده از هدفون به مدت یک ثانیه با مکث 1.5 ثانیه ای برای شنوندگان پخش می شدند.
از آزمودنی ها خواسته می شد تا مشخص کنند که صدای پخش شده بالا، پایین یا برابر با صدای مرجع است. این کار منجر به ایجاد گروهی از منحنی ها به نام منحنی های فلچر-مانسون شده است.
در سال 1956 رابینسون و دادسون اندازهگیریهای فلچر-مونسون را تکرار کردند، این بار با استفاده از بلندگوها در یک اتاق صامت. منحنی های رابینسون-دادسون به دست آمده در شکل زیر نشان داده شده است. پایین ترین این منحنی ها آستانه شنوایی است.
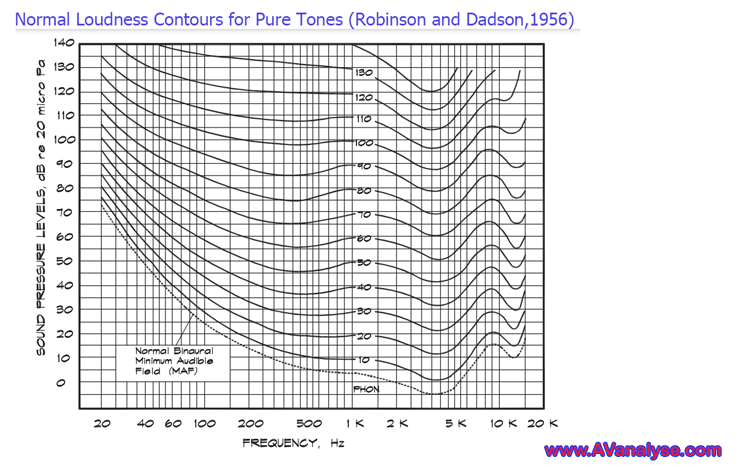
نکته جالبی که در این سطوح وجود دارد این است که در منحنی آستانه شنوایی مشاهده می کنیم که در سطح صفر دسی بل وقتی از فرک 2000 هرتز جلوتر می رویم منحنی به زیر صفر دسی بل وارد می شود و این افت در فرکانس 3150 هرتز به بیشترین مقدار می رسد، این فرکانس همان فرکانسی است که گوش بیشترین حساسیت را دارد.
همچنین این نمودار نشان می دهد که شنوایی انسان به طور قابل توجهی به صداهای فرکانس پایین حساسیت کمتری دارد.
در این منحنی ها همچنین مشاهده می کنیم که در فرکانسهای پایینتر، با کاهش فرکانس، سطح تراز صدا بالا میرود بطوریکه در فرکانس 30 هرتز، سطح شدت به حدود 65 دسیبل می رسد.
مشاهده می کنیم که با افزایش شدت صدا، پاسخ فرکانسی گوش صاف تر می شود. در محدوده تقریباً 100 دسی بل پاسخ گوش تقریباً هموار می شود اما هنچنان در محدوده فرکانس 3150 هرتز حساسیت بیشتر است. منحنی های این شکل منحنی های با بلندی یکسان نامیده می شوند.
برای همه نقاط در امتداد هر یک از این منحنی ها بلندی صدا یکسان است. یک سطح بلندی صدا (با واحد فون) به هر منحنی تخصیص داده می شود که از نظر عددی برابر با سطح شدت صدای آن منحنی در 1000 هرتز است. بنابراین اگر منحنی 40 فون را دنبال کنیم، میبینیم که صدایی با شدت 50 دسیبل در 100 هرتز دارای سطح بلندی 40 فون است. در 1000 هرتز سطح بلندی صدا با سطح شدت صدا برابر است. در 10000 هرتز سطح شدت صدا حدود 46 دسی بل است که بلندی آن نیز همان 40 فون است.
خطوط سطح بلندی نسبی سیگنال صوتی بر اساس قضاوت انسان در مورد بلندی مطلق صدا است. بر اساس یک مقایسه نسبی می توان سؤالی را مطرح کرد و آن این که «چه زمانی بلندی صدا دو برابر می شود؟» این باعث می شود تا اندازه ای از بلندی نسبی با واحد سون (Sone) وجود داشته باشد.
در این طرح متریک انتخاب شده خطی است. صدایی با بلندی نسبی 2 سون دو برابر بلندتر از صدای 1 سون است. خط مبنا منحنی 40 فون است که به آن مقدار 1 سون داده می شود. شکل زیر نیز رابطه بین بلندی نسبی صدا در سون ها و سطح بلندی صدا در فون ها را نشان می دهد.
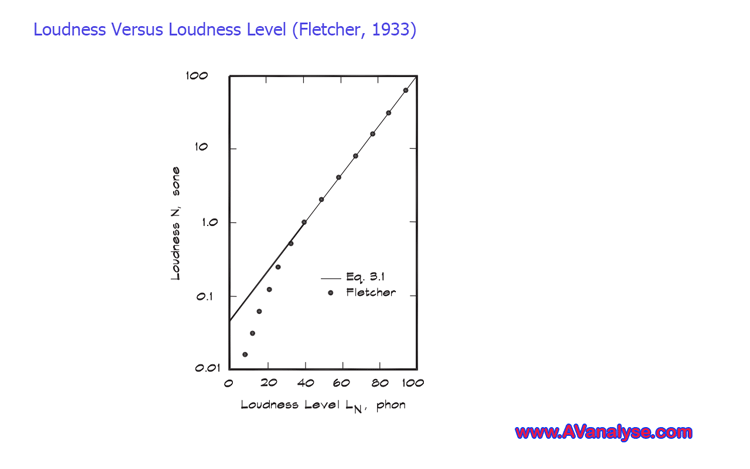
سخن پایانی اینکه در این پست سعی شد بصورت مختصر و مفید مفهوم بلندی صدا و نحوه اندازه گیری آن شرح داده شود. در پایان و در یک جمله می توان گفت برای این منظور می توانیم از منحنی های فلچر-مانسون کمک بگیریم.
برای مطالعه بیشتر استانداردهای زیر پیشنهاد می شود.
ISO 532-1:2017 Acoustics — Methods for calculating loudness — Part 1: Zwicker method
ISO 226:1987 Acoustics — Normal equal-loudness level contours
Recommendation ITU-R BS.1770-2
