برای مدت طولانی، استفاده از رایانه برای پردازش یک تصویر دیجیتال کاری بود که تنها توسط گروه نسبتاً کوچکی از متخصصان انجام می توانست انجام شود. گروهی که به تجهیزات گران قیمت دسترسی داشتند. معمولاً این ترکیب از متخصصان و تجهیزات را فقط در آزمایشگاههای تحقیقاتی میتوان یافت و بنابراین زمینه پردازش تصویر دیجیتال ریشه در صنعت و دانشگاه دارد.
سالهای پیش خوب بخاطر داریم که دیجیتالی کردن یک عکس و ذخیره آن در یک فایل روی رایانه کاری زمانبر بود، شاید تصور این امر دشوار باشد، اما یادآوری این موضوع که کامپیوترهای شخصی در اوایل دهه ۱۹۹۰ به اندازه کافی قدرتمند نبودند که حتی یک بار آنرا در حافظه اصلی بارگذاری کنند، برای ما که در زمان انتقال از یک نسل تکنولوژی به دیگر زندگی کرده ایم بسیار خاطره انگیز است.
امروزه با گسترش تجهیزات ارتباطی مختلف و وجود سیستم های پردازشی قدرتمند در این تجهیزات تقریبا همه افراد در طول روز به نوعی با تصاویر دیجیتال سرو کار دارند. هر زمان که ما در حال استفاده از تصاویر دیجیتال هستیم به نوعی در حال استفاده از سیستم های مبتنی بر پردازش تصویر دیجیتال هستیم. در نتیجه، پردازش تصویر دیجیتال به امری گریز ناپذیر برای تجهیزات مختلف شده است. بسته های سخت افزاری و نرم افزاری قدرتمند امکان ویرایش تصاویر و ویدئوهای دیجیتال را برای همه فراهم کرده است.
پیشرفت های بوجود آمده در تجهیزات مختلف در زمینه گرفتن تصاویر دیجیتال و پردازش آن منجر به این شده است که تقریبا همه افراد در طول روز بسیاری از امور خود را با سیستم هایی که به نوعی تصاویر دیجیتال را خلق و یا پردازش می کنند سر و کار دارند. خوشبختانه برای استفاده های روزمره و عمومی نیازی به دانش بسیار بالایی از نحوه انجام پردازش های تصویر نیست ، همانطور که درک عمیق موتور احتراقی برای راندن موفقیت آمیز یک ماشین غیر ضروری است.
با این حال، متخصصان فناوری اطلاعات باید بیش از پیش با پردازش تصویر دیجیتال آشنا باشند. از آنها انتظار می رود که بتوانند تصاویر و رسانه های دیجیتال مرتبط را کنکاش کرده درک نموده و ارتقا دهند. به همین نحو مهندسان نرم افزار و دانشمندان کامپیوتر به طور فزاینده ای با برنامه ها، پایگاه های داده و سیستم های مرتبط در حال توسعه مواجه می شوند که باید به درستی با تصاویر دیجیتال برخورد کنند.
فقدان تجربه عملی و دانش مورد نیاز متخصصان در این زمینه به علاوه درک غالباً نامشخص از مبانی اساسی آن و دست کم گرفتن مشکلات احتمالی در این زمینه، اغلب منجر به راهحلهای ناکارآمد، خطاهای پرهزینه و آسیب ها و ضرر های جبران ناپذیری میشود. از این رو به نوعی تمام متخصصانی که به نوعی با تصاویر دیجیتال سرو کار دارند ضروری است بسته به نیاز خود با دانش پردازش تصاویر دیجیتال آشنایی داشته باشند.
هر زمان که ما در حال ویرایش یک تصویر دیجیتال هستیم در واقع به نوعی در حال استفاده از یک برنامه ویرایش تصویر دیجیتال هستیم که بر اساس الگوریتم های پردازش تصویر نوشته شده است. نرم افزارهایی همچون Adobe Photoshop یا Corel Paint نرم افزارهایی هستند که کار ویرایش تصویر را بر اساس الگوریتم های پردازش تصویر انجام می دهند.
از سوی دیگر، مفهوم، طراحی، توسعه، و بهبود برنامه های تصویربرداری دیجیتال، محیط های برنامه نویسی مدرن، با API های گسترده خود (رابط برنامه نویسی کاربردی)، عملاً همه جنبه های پردازشی را، اعم از شبکه، پایگاه داده، گرافیک، یا تصویربرداری، را به راحتی در دسترس قرار می دهند.
امروزه متخصصان گرافیک تمایل دارند به موضوعاتی مانند واقع گرایی و مخصوصاً از نظر بازی های رایانه ای، سرعت رندر علاقه مند شوند، این رشته از تعدادی روش استفاده می کند که از پردازش تصویر منشا می گیرند، مانند تبدیل تصویر (مورفینگ)، بازسازی مدلهای سهبعدی از دادههای تصویر، و تکنیکهای تخصصی مانند رندر مبتنی بر تصویر.
منظور از تصاویر شطرنجی تصاویری هستند که از عناصر تصویری تشکیل شدهاند که معمولاً به عنوان پیکسل شناخته میشوند و در یک شبکه مستطیلی منظم چیده شدهاند. هر روز، افراد با طیف گسترده ای از تصاویر شطرنجی دیجیتال کار می کنند مانند عکس های رنگی از افراد و مناظر، اسکن اسناد چاپی، نقشه های ساختمانی، اسناد فکس شده، اسکرین شات ها، تصاویر پزشکی مانند اشعه ایکس و سونوگرافی، و بسیاری دیگر. علیرغم همه منابع مختلف برای این تصاویر، همه آنها معمولاً در نهایت به صورت آرایه های مرتب شده مستطیلی از عناصر تصویر نشان داده می شوند. در زیر انواعی از تصاویر دیجیتال شطرنجی آورده شده است.
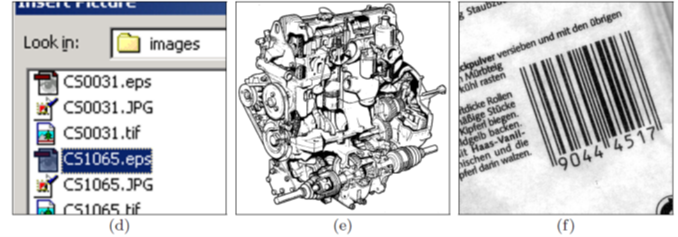
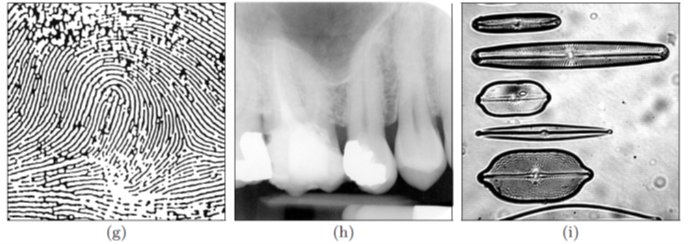
در شکل ۱ نمونه ای از تصاویر دیجیتال از نوع منظره طبیعی (a)، رندر با نرم افزارهای طراحی (b)، پوستر با نرم افزار گرافیکی (c)، اسکرین شات کامپیوتر (d)، تصویر سیاه و سفید (e)، بارکد (f)، اثر انگشت (g)، اشعه ایکس ( h)، اسلاید میکروسکوپ (i)، تصویر ماهواره ای (j)، تصویر رادار مصنوعی (k)، شی نجومی (l) را مشاهده می کنیم.


تهیه تصویر خود تاریخ بسیار پر فراز ونشیبی دارد و دوربین های عکاسی از ابتدا تا کنون بسیار تکامل یافته و در سال های اخیر با دیجیتال شدن آنها انقلابی در این صنعت ایجاد شده است. از این رو فرآیندی که طی آن یک صحنه به یک تصویر دیجیتال تبدیل میشود، فرآیندی بسیار عمیق، متنوع و پیچیده است. در ادامه در مورد یکی از اولین مدل های دوربین عکاسی یعنی دروبین Pinhole و نحوه کار آن مقداری توضیح خواهیم داد.
دوربین پینهول یکی از سادهترین مدلهای دوربین است و از قرن سیزدهم، زمانی که به نام Camera Obscura شناخته میشد، مورد استفاده قرار گرفت.
در حالی که دوربین های Pinhole امروزه به جز برای علاقه مندان کاربرد عملی ندارند، آنها مدلی مفید برای درک اجزای نوری ضروری یک دوربین ساده هستند. دوربین پین هول شامل یک جعبه بسته با یک دهانه کوچک در قسمت جلویی است که نور از آن وارد می شود و تصویری را روی دیوار مقابل تشکیل می دهد. نور یک تصویر کوچکتر و معکوس از صحنه را تشکیل می دهد (شکل ۲).
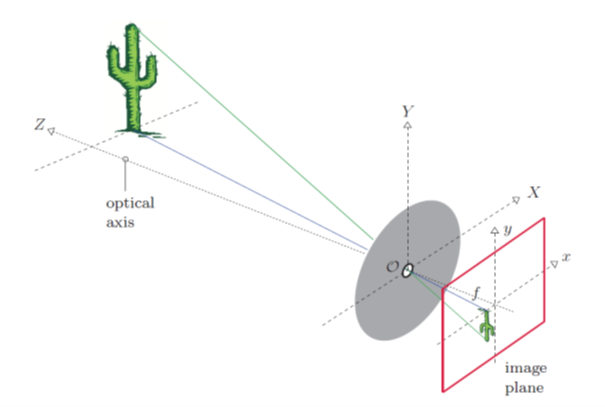
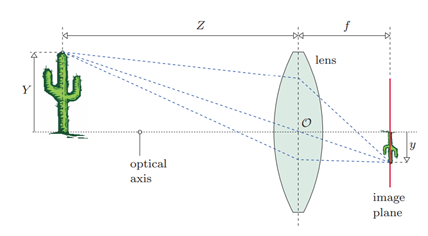
ویژگی های هندسی دوربین پین هول بسیار ساده است. محور نوری از روزنه عبور کرده و عمود بر صفحه تصویر عبور است. ما یک جسم قابل مشاهده (کاکتوس در شکل ۱) را در فاصله افقی Z از سوراخ سوزنی و فاصله عمودی Y از محور نوری فرض می کنیم. ارتفاع طرح y توسط دو پارامتر تعیین می شود: عمق (ثابت) جعبه دوربین f و فاصله Z جسم از مبدا سیستم مختصات. با تطبیق مثلث های مشابه، روابط بین مختصات سه بعدی شی X، Y، Z و مختصات تصویر مربوطه x، y در یک فاصله کانونی معین f را به دست می آوریم:
(۱) X=-f Y/Z Y=-f X/Z
بدیهی است که به روشی مشابه نحوه تعیین بزرگنمایی تصویر، با فاصله کانونی f مقیاس تصویر به دست آمده متناسب با فاصله کانونی f تغییر می کند. برای یک صحنه ثابت، یک f کوچک (یعنی فاصله کانونی کوتاه) منجر به یک تصویر کوچک و یک زاویه دید بزرگ میشود، درست مانند زمانی که از لنز واید استفاده میشود.
در مقابل، افزایش “فاصله کانونی” f منجر به تصویر بزرگتر و زاویه دید کمتری می شود که مشابه اثر یک لنز تله فوتو است.
علامت منفی در معادله (۱) به این معنی است که تصویر نمایش داده شده در جهت افقی و عمودی برگردانده می شود. معادله (۱) چیزی را توصیف می کند که معمولاً به عنوان “تبدیل پرسپکتیو” از مختصات تصویر سه بعدی به دو بعدی شناخته می شود.
ویژگیهای مهم این مدل نظری، از جمله این که خطوط مستقیم در فضای سهبعدی همیشه به خطوط مستقیم در برآمدگیهای دو بعدی نگاشت میشوند و دایرهها به صورت بیضی ظاهر میشوند.
در حالی که هندسه ساده دوربین پین هول آن را برای درک اصول اولیه آن مفید می کند، اما هرگز در عمل واقعاً استفاده نمی شود. یکی از مشکلات دوربین پین هول این است که برای ایجاد یک تصویر واضح به یک دهانه بسیار کوچک نیاز دارد. این به نوبه خود میزان نور عبوری را به شدت محدود می کند و در نتیجه منجر به زمان نوردهی بسیار طولانی می شود.
در دوربین های امروزی از لنزهای شیشه ای یا سیستم لنزهای نوری استفاده می شود که خواص نوری آنها در بسیاری از جنبه ها بسیار برتر است، اما البته بسیار پیچیده تر نیز هستند.
همانطور که در شکل ۳ نشان داده شده است، همچنان میتوانیم مدل خود را واقعیتر کنیم، بدون اینکه پیچیدگی آن را افزایش دهیم. در این مدل، عدسی متقارن و بی نهایت نازک در نظر گرفته می شود، به طوری که تمام پرتوهای نوری که از آن عبور می کنند در یک صفحه مجازی در وسط عدسی شکسته می شوند.
هندسه تصویر حاصل عملاً همانند تصویر دوربین پین هول است. این مدل به اندازه کافی پیچیده نیست که جزئیات فیزیکی سیستمهای لنز واقعی، مانند اعوجاجهای هندسی و خواص انکساری متمایز رنگهای مختلف را در بر بگیرد.
آنچه در صفحه تصویر دوربین ما نمایش داده می شود اساساً یک توزیع دو بعدی، وابسته به زمان و با توزیع پیوسته انرژی نور است. برای به دست آوردن یک “عکس فوری دیجیتال” از این توزیع نور پیوسته در حال تغییر رایانه باید سه مرحله اصلی زیر را پردازش نماید:
۱. توزیع نور پیوسته باید به صورت فضایی نمونه برداری شود.
۲. نتایج این تابع “گسسته” باید در حوزه زمان نمونه برداری شوند تا یک تصویر واحد ایجاد شود.
۳. در نهایت، مقادیر به دست آمده باید به مجموعه محدودی از مقادیر عددی کوانتیزه شوند تا در رایانه قابل نمایش باشند.
نمونه برداری فضایی از یک تصویر یعنی تبدیل یک سیگنال پیوسته به نمایشی که بیانگر آن تصویر اما بصورت گسسته است.
این نمونه برداری به هندسه عناصر حسگر دستگاه (به عنوان مثال، دوربین دیجیتال یا فیلمبرداری) بستگی دارد.
عناصر حسگر منفرد معمولاً به صورت یک آرایه مستطیل شکل بر روی صفحه حسگر مرتب می شوند (شکل ۴). انواع دیگری از سنسورهای تصویر که شامل عناصر شش ضلعی و ساختارهای حسگر دایره ای می شوند را می توان در محصولات تخصصی دوربین ها یافت.
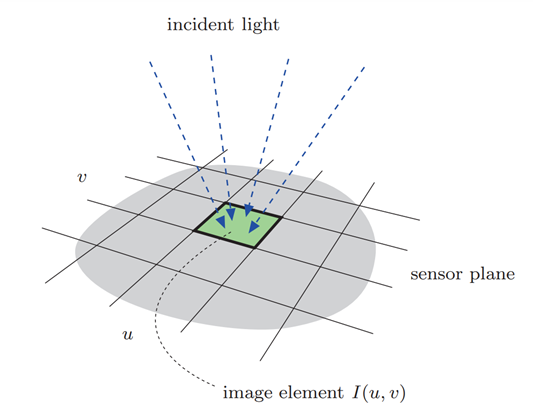
نمونه برداری زمانی با اندازه گیری در فواصل زمانی معین میزان تابش نور به هر عنصر حسگر منفرد انجام می شود. سنسور CCD2 یا CMOS3 در یک دوربین دیجیتال این کار را با ایجاد فرآیند شارژ الکتریکی انجام می دهد. این سنسور توسط جریان پیوسته فوتون ها القا می شود و سپس میزان باری که در هر عنصر حسگر و در طول زمان نوردهی ایجاد می شود را اندازه گیری می کند.
به منظور ذخیره و پردازش مقادیر تصویر در رایانه، آنها معمولاً به محدوده ای از مقادیر صحیح تبدیل می شوند (مثلاً ۲۵۶ = 2۸ یا ۴۰۹۶ = 2۱۲).
گاهی اوقات از مقیاس floating-point در کاربردهای حرفه ای مانند تصویربرداری پزشکی استفاده می شود. تبدیل با استفاده از مبدل آنالوگ به دیجیتال انجام می شود که معمولاً مستقیماً در قسمت الکترونیکی سنسور تعبیه شده است یا توسط سخت افزار رابط ویژه انجام می شود.
نتیجه سه مرحله بخش قبل توصیف تصویر در قالب یک ماتریس دو بعدی از اعداد صحیح است (شکل ۵). به طور رسمی تر، یک تصویر دیجیتال I یک تابع دو بعدی از مختصات اعداد صحیح N × N است که به طیفی از تصاویر ممکن (پیکسل) مقادیر P نگاشت می شود، به طوری که:
u, v ∈ N
I(u, v) ∈ P
اکنون ما آماده ایم تصویر را به کامپیوتر خود انتقال دهیم و آن را به هر شکلی که می خواهیم فشرده، ذخیره یا ویرایش کنیم. در این مرحله، دیگر برای ما مهم نیست که تصویر چگونه ایجاد شده است، زیرا اکنون یک آرایه دو بعدی ساده از اعداد است. اما قبل از حرکت به چند تعریف مهم دیگر نیاز داریم.

در ادامه، تصاویر مستطیلی را فرض می کنیم، و در حالی که این یک فرض نسبتا مطمئن است، استثناهایی وجود دارد. اندازه یک تصویر مستقیماً از عرض M (تعداد ستونها) و ارتفاع N (تعداد ردیف) ماتریس تصویر I تعیین میشود.
وضوح تصویر یا رزولوشن ابعاد فضایی تصویر را در دنیای واقعی مشخص میکند و به عنوان تعداد عناصر تصویر در هر اندازه گیری داده می شود. به عنوان مثال، نقطه در هر اینچ (dots per inch) یا (dpi) یا خطوط در اینچ (lines per inch) یا (lpi) برای تصاویر چاپی، یا بر حسب پیکسل در هر کیلومتر برای تصاویر ماهواره ای.
در اکثر موارد، وضوح تصویر در جهت افقی و عمودی یکسان است، به این معنی که عناصر تصویر مربع هستند. توجه داشته باشید که همیشه اینطور نیست، به عنوان مثال، سنسورهای تصویر اکثر دوربین های فیلمبرداری فعلی دارای پیکسل های غیر مربعی هستند!
وضوح فضایی یک تصویر ممکن است در بسیاری از مراحل اولیه پردازش تصویر، مانند عملیات نقطه ای یا فیلترها، مرتبط نباشد. با این حال، اطلاعات وضوح دقیق در مواردی که عناصر هندسی مانند دایرهها باید روی یک تصویر کشیده شوند یا فاصلههای درون تصویر باید اندازهگیری شود، مهم است. به این دلایل، اکثر فرمتهای تصویر و سیستمهای نرمافزاری که برای کاربردهای حرفهای طراحی شدهاند، به اطلاعات دقیق در مورد وضوح تصویر متکی هستند.
برای اینکه بدانیم کدام موقعیت روی تصویر با کدام عنصر تصویر مطابقت دارد، باید یک سیستم مختصات را اعمال کنیم. برخلاف قراردادهای معمول ریاضی، در پردازش تصویر، سیستم مختصات معمولاً در جهت عمودی چرخانده میشود. یعنی مختصات y از بالا به پایین اجرا می شود و مبدأ در گوشه سمت چپ بالا قرار دارد (شکل ۶). در حالی که این سیستم هیچ مزیت عملی یا نظری ندارد و در واقع ممکن است در زمینه تبدیل های هندسی کمی گیج کننده باشد، تقریبا بدون استثنا در سیستم های نرم افزاری تصویربرداری استفاده می شود.
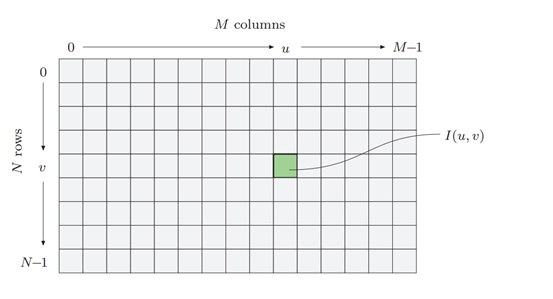
ظاهراً این سیستم ریشه در طراحی اولیه سیستمهای پخش تلویزیونی دارد، جایی که ردیفهای تصویر در امتداد انحراف عمودی پرتو الکترونی شمارهگذاری میشوند که از بالا به پایین صفحه نمایش حرکت میکرد. ما به دلایل عملی شماره گذاری سطرها و ستون ها را از صفر شروع می کنیم، زیرا در برنامه جاوا Java نمایه سازی آرایه ها نیز از صفر شروع می شود.
اطلاعات درون یک عنصر تصویر به نوع داده مورد استفاده برای نمایش آن بستگی دارد. مقادیر پیکسل عملاً همیشه کلمات دودویی به طول k هستند به طوری که یک پیکسل می تواند هر یک از ۲k مقدار مختلف را نشان دهد.
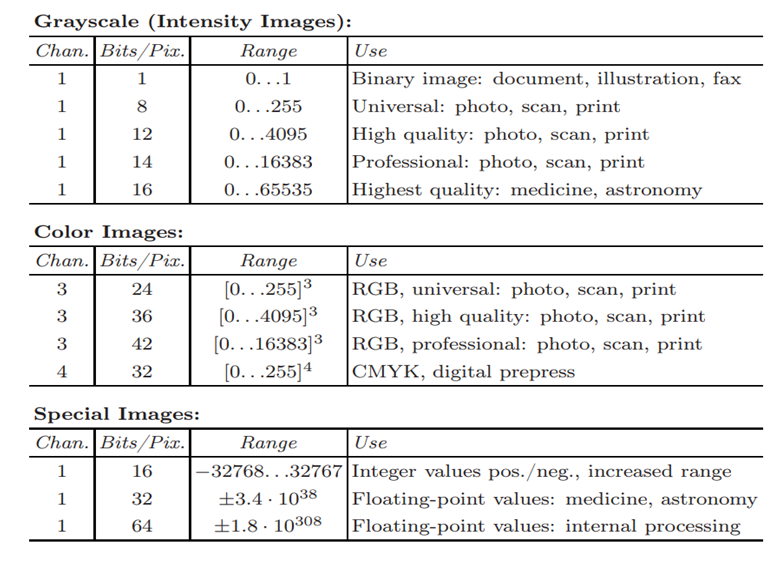
مقدار k عمق بیت (یا فقط “عمق”) تصویر نامیده می شود. طرح دقیق سطح بیت هر پیکسل به نوع تصویر بستگی دارد. به عنوان مثال، رنگ باینری، خاکستری، یا رنگ RGB.
داده های تصویر در یک تصویر در مقیاس خاکستری از یک کانال تشکیل شده است که شدت، روشنایی یا چگالی تصویر را نشان می دهد. در بیشتر موارد، فقط مقادیر مثبت معنا دارند، زیرا اعداد نشان دهنده شدت انرژی نور یا چگالی فیلم هستند و بنابراین نمی توانند منفی باشند، بنابراین معمولاً از اعداد صحیح کامل در محدوده [۰,…, ۲k-1] استفاده می شود.
به عنوان مثال، یک تصویر معمولی در مقیاس خاکستری از k = 8 بیت (۱ بایت) در هر پیکسل و مقادیر شدت در محدوده [۰,…,۲۵۵] استفاده می کند، جایی که مقدار ۰ نشان دهنده حداقل روشنایی (سیاه) و ۲۵۵ حداکثر روشنایی ( سفید) است.
برای بسیاری از کاربردهای حرفه ای عکاسی و چاپ، و همچنین در پزشکی و نجوم، ۸ بیت در هر پیکسل کافی نیست. عمق تصویر ۱۲، ۱۴ و حتی ۱۶ بیتی اغلب در این حوزه ها مشاهده می شود.
توجه داشته باشید که عمق بیت معمولاً به تعداد بیت های مورد استفاده برای نمایش یک جزء رنگی اشاره دارد، نه تعداد بیت های مورد نیاز برای نمایش یک پیکسل رنگی کامل.
به عنوان مثال، یک تصویر رنگی رمزگذاری شده با RGB با عمق 8-bitبه ۸ بیت برای هر کانال برای مجموع ۲۴ بیت نیاز دارد، در حالی که همان تصویر با عمق ۱۲-bit بیت در مجموع به ۳۶ بیت نیاز دارد. (جدول ۱)
تصاویر باینری نوع خاصی از تصویر بر مبنای شدت هستند که در آن پیکسل ها فقط می توانند یکی از دو مقدار سیاه یا سفید را بگیرند. این مقادیر معمولاً با استفاده از یک بیت واحد صفر یا یک در هر پیکسل کدگذاری می شوند. تصاویر باینری اغلب برای نمایش گرافیک خطی، آرشیو اسناد، رمزگذاری ارسال فکس و البته در چاپ الکترونیکی استفاده می شوند. (جدول ۱)
اکثر تصاویر رنگی بر اساس رنگهای اصلی قرمز، سبز و آبی (RGB) هستند که معمولاً از ۸ بیت برای هر جزء رنگی استفاده میکنند. در این تصاویر هر پیکسل برای رمزگذاری هر سه جزء به ۳×۸ = 24 بیت نیاز دارد و محدوده هر جزء رنگی مجزا [۰,…,۲۵۵] است.
همانند تصاویر بر مبنای شدت، تصاویر رنگی با ۳۰، ۳۶ و ۴۲ بیت در هر پیکسل معمولاً در برنامه های حرفه ای استفاده می شوند. در نهایت، در حالی که اکثر تصاویر رنگی شامل سه جزء هستند، تصاویر با چهار یا چند جزء رنگی در اکثر برنامه های پیش از چاپ معمول هستند.
تصاویر نمایه شده یا پالت یک کلاس بسیار ویژه از تصاویر رنگی را تشکیل می دهند. تفاوت بین یک تصویر نمایه شده و یک تصویر رنگی واقعی در تعداد رنگ های مختلف است که می توان در یک تصویر خاص استفاده کرد. (جدول ۱)
اگر هیچ یک از فرمت های استاندارد بالا برای نمایش مقادیر تصویر کافی نباشد، این نوع فرمت استفاده می شود. دو نمونه رایج از تصاویر خاص، آنهایی هستند که مقادیر منفی دارند و آنهایی که دارای مقادیر ممیز شناور هستند. تصاویر با مقادیر منفی در طول مراحل پردازش تصویر، مانند فیلتر کردن برای تشخیص لبه ، و تصاویر با مقادیر ممیز شناور اغلب در کاربردهای پزشکی، بیولوژیکی یا نجومی یافت می شوند، جایی که محدوده عددی گسترده و دقت مورد نیاز است. این فرمتهای خاص عمدتاً مختص برنامههای کاربردی هستند و بنابراین ممکن است استفاده از ابزارهای استاندارد پردازش تصویر دشوار باشد. (جدول ۱)